Características de transferência

Em transistores, as características de transferência podem ser entendidas como a plotagem de uma corrente de saída em relação a uma magnitude de controle de entrada, que consequentemente exibe uma “transferência” direta de variáveis ​​de entrada para saída na curva representada no gráfico.

Sabemos que para um transistor de junção bipolar (BJT), a corrente do coletor de saída IC e a corrente de base de entrada de controle IB estão relacionadas pelo parâmetro beta , que é considerado constante para uma análise.

Referindo-se à equação abaixo, encontramos uma relação linear existente entre IC e IB. Se tornarmos o nível de IB 2x, o IC também dobra proporcionalmente.

Mas, infelizmente, essa relação linear conveniente pode não ser alcançável em JFETs em suas magnitudes de entrada e saída. Em vez disso, a relação entre o ID da corrente de drenagem e a tensão da porta VGS é definida por Equação de Shockley :

Aqui, a expressão quadrada torna-se responsável pela resposta não linear ao longo do ID e VGS, o que dá origem a uma curva que cresce exponencialmente, à medida que a magnitude do VGS diminui.

Embora uma abordagem matemática seja mais fácil de implementar para a análise dc, a forma gráfica pode exigir a representação gráfica da equação acima.

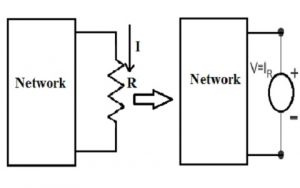
Isso pode apresentar o dispositivo em questão e a plotagem das equações da rede relacionadas às variáveis ​​idênticas.

Encontramos a solução observando o ponto de intersecção das duas curvas.

Lembre-se de que quando você usa o método gráfico, as características do dispositivo não são afetadas pela rede onde o dispositivo está implementado.

Conforme a intersecção entre as duas curvas muda, ela também muda a equação da rede, mas isso não tem efeito na curva de transferência definida pela Eq, 5.3 acima.

Portanto, em geral, podemos dizer que:

A característica de transferência definida pela Equação de Shockley não é afetada pela rede onde o dispositivo é implementado.

Podemos obter a curva de transferência usando a equação de Shockley ou a partir das características de saída conforme ilustrado na Fig. 5.10

Na figura abaixo, podemos ver dois gráficos. A linha vertical mede miliamperes para os dois gráficos.

Um gráfico representa a corrente de dreno ID versus tensão dreno-fonte VDS, o segundo gráfico representa a corrente dreno versus tensão porta-fonte ou ID vs VGS.

Com a ajuda das características do dreno mostradas no lado direito do eixo 'y', podemos traçar uma linha horizontal começando na região de saturação da curva mostrada como VGS = 0 V até o eixo mostrado como ID.

Os níveis atuais assim alcançados para os dois gráficos é IDSS.

O ponto de intersecção na curva de ID vs VGS será o dado abaixo, porque o eixo vertical é definido como VGS = 0 V

Observe que as características do dreno mostram a relação entre uma magnitude de saída do dreno com outra magnitude de saída do dreno, em que os dois eixos são interpretados por variáveis ​​na mesma região das características do MOSFET.

Assim, as características de transferência podem ser definidas como um gráfico de uma corrente de drenagem MOSFET versus uma quantidade ou um sinal atuando como um controle de entrada.

Consequentemente, isso resulta em uma 'transferência' direta entre as variáveis ​​de entrada / saída, quando a curva é usada à esquerda da Fig 5.15. Se fosse uma relação linear, o gráfico de ID vs VGS teria sido uma linha reta entre IDSS e VP.

No entanto, isso resulta em uma curva parabólica devido ao espaçamento vertical entre o passo do VGS sobre as características do dreno, que diminui em uma extensão apreciável à medida que o VGS fica cada vez mais negativo, na Fig. 5.15.

Se compararmos o espaço entre VGS = 0 V e VGS = -1V com aquele entre VS = -3 V e o pinch-off, vemos que a diferença é idêntica, embora seja muito diferente para o valor de ID.

Podemos identificar outro ponto na curva de transferência desenhando uma linha horizontal da curva VGS = -1 V até o eixo de ID e, posteriormente, estendendo-a para o outro eixo.

Observe que VGS = - 1V no eixo inferior da curva de transferência quando ID = 4,5 mA.

Observe também que, na definição de ID em VGS = 0 V e -1 V, os níveis de saturação de ID são usados, enquanto a região ôhmica é desprezada.

Seguindo adiante, com VGS = -2 V e - 3V, podemos terminar o gráfico da curva de transferência.

Como aplicar a equação de Shockley

Você também pode obter diretamente a curva de transferência da Fig 5.15 aplicando a Equação de Shockley (Eq.5.3), desde que os valores de IDSS e Vp sejam fornecidos.

Os níveis de IDSS e VP definem os limites da curva para os dois eixos e requer apenas a plotagem de alguns pontos intermediários.

A genuinidade do Equação de Shockley Eq.5.3 como uma fonte da curva de transferência da Fig 5.15 pode ser perfeitamente expressa inspecionando certos níveis distintos de uma variável particular e, em seguida, identificando o nível correspondente da outra variável, da seguinte maneira:

Isso corresponde ao gráfico mostrado na Fig.5.15.

Observe com que cuidado os sinais negativos para VGS e VP são gerenciados nos cálculos acima. A omissão de até mesmo um único sinal negativo pode levar a um resultado totalmente errado.

É bastante claro a partir da discussão acima, que se tivermos os valores de IDSS e VP (que podem ser consultados na folha de dados), podemos determinar rapidamente o valor de ID para qualquer magnitude de VGS.

Por outro lado, por meio da Álgebra padrão, podemos derivar uma equação (via Eq.5.3), para o nível VGS resultante para um determinado nível de ID.

Isso poderia ser derivado de forma bastante simples, para obter:

Agora vamos verificar a equação acima determinando o nível de VGS que produz uma corrente de dreno de 4,5 mA para um MOSFET com as características correspondentes à Fig 5.15.

O resultado verifica a equação de acordo com a Fig.5.15.

Usando o método abreviado

Visto que precisamos plotar a curva de transferência com bastante frequência, pode ser conveniente obter uma técnica abreviada para plotar a curva. Um método desejável seria permitir ao usuário traçar a curva de forma rápida e eficiente, sem comprometer a precisão.

A equação 5.3 que aprendemos acima é projetada de forma que níveis particulares de VGS produzam níveis de ID que podem ser lembrados para utilização como pontos de plotagem ao desenhar a curva de transferência. Se especificarmos VGS como 1/2 do valor de pinch-off VP, o nível de ID resultante pode ser determinado usando a equação de Shockley da seguinte maneira:

Deve-se notar que a equação acima não foi criada para um nível específico de VP. A equação é uma forma geral para todos os níveis de VP enquanto VGS = VP / 2. O resultado da equação sugere que a corrente de dreno será sempre 1/4 do nível de saturação IDSS, desde que a tensão porta-fonte tenha um valor que é 50% menor que o valor de pinch-off.

Observe que o nível de ID para VGS = VP / 2 = -4V / 2 = -2V de acordo com a Fig.5.15

Optando por ID = IDSS / 2 e substituindo-o na Eq.5.6, obtemos os seguintes resultados:

Embora mais pontos numéricos possam ser estabelecidos, um nível suficiente de precisão pode ser alcançado simplesmente desenhando a curva de transferência usando apenas 4 pontos de plotagem, conforme identificado acima e também na Tabela 5.1 abaixo.

Na maioria dos casos, podemos empregar apenas o ponto do gráfico usando VGS = VP / 2, enquanto as interseções do eixo em IDSS e VP nos darão uma curva suficientemente confiável para a maioria das análises.